皆さん,第1回目の課題はいかがでしたか。慶応塾高の地学は「地球の大きさを歩測で測る」, から毎年はじまります。実際にGPSを使って外でやる方が面白いのですが,誰か 小林晋平先生(学芸大)の動画 を見て試してみませんか。
なんと今から2200年も前に,GPSも使わずに,基本的には同じ方法でエラトステネスは 地球の大きさのみならず,さらに月の大きさと,月までの距離までも明らかにしてしまったの です。まず地球が丸いことは月食が太陽の反対に月が来たときに起こることから,それが 地球の影であり,分かっていました(写真)。エラトステネスは,この月食という現象から月の大きさを割り出したのです(月食がこんな写真 みたいに見えたら誰でもすぐ分かりますよ。) 結構な頻度で月食はおこりますが,次のようなことが 知られていました。月が欠け始めてから完全に影に入るまでが約50分。そこから再び月が現われ て,完全にもとの月になる(影から出る)までが,200分でした。さて,地球の影の直径は月の 直径の何倍ですか?(影の中央をすぎていく時の場合で,地球の影の大きさ=地球の大きさ,と します 答え→ 200÷50で およそ4倍)。 このようにして月の実際の大きさが分かったら,月までの距離も分かりますよね。どうやって?。 自分の目と手と定規で,相似の関係を使うのです。月が出ているときに,手を伸ばして,親指と 人差し指の間で月の直径を測ります。仮に,5mmだったとして,手を伸ばした目からの長さが, 60cmだったら,月までの距離は,(月の実際の直径)÷5mm×60cmということになります。
ちなみに,この月の見える大きさを視直径といいます。5円玉の穴がちょうど5mmなので,この つぎ月が見えたら試してみてください。手を伸ばした,5円玉の穴に,月はすっぽりと入ってしまう はずです。(50円硬貨の穴は4mm)。長さ60cmの底辺の高さ5mmの三角形の角度 はtanθ=0.5/60ですが,この角度0.5°(30′)が月の視直径(太陽もほぼ同じ)です。 この比で月までの距離が求まるということです。分かりましたでしょうか?
(設問:頭の体操)
17両編成の長さ400mの新幹線が,秒速80m(時速約290km)で,あるトンネルを通過する (最後の車両が出る)のに,10秒間かかりました。このトンネルの長さは何mですか?
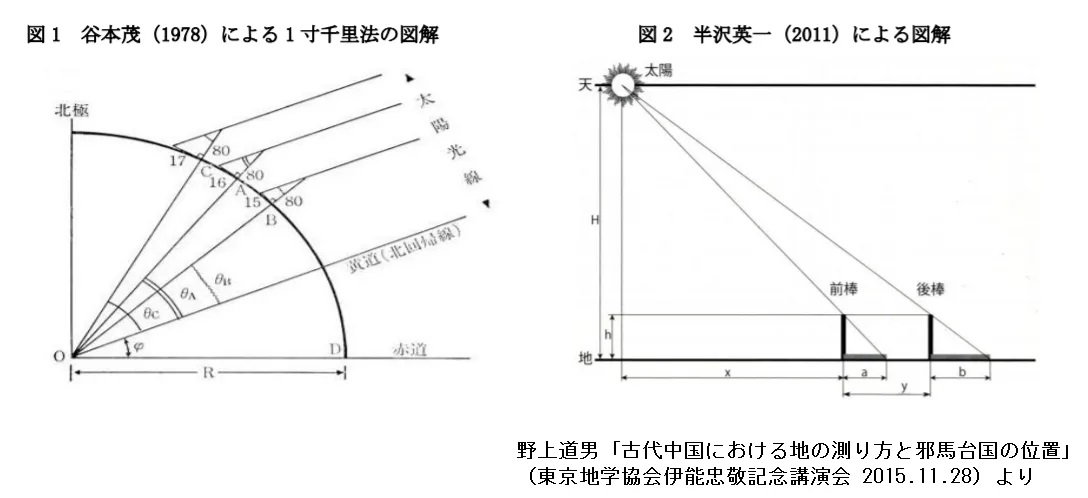
ところで,地球が丸い,という認識はいつ頃から広まったのでしょうか。これはひとつの例で すが,中国の場合,西暦500年頃までは,蓋天説(その後,渾天説=球体になる)といって地球を平面(空も天井のように) と考えていました。ところが,広い中国では,北と南では(緯度を移動すると)太陽の南中高度が 変わることに気づきました。それを利用して,距離を測ることにしたのです。太陽高度(角度)を 測る基本は,棒を立て,影の長さを測る(世界共通)ことで,その影の長さが1寸(約3cm)違えば 千里に相当する(一寸千里)としました。
有名な邪馬台国論争では,中国から日本への行程が問題になりますが,この当時の地理概念が この古い距離単位に関わることが論じられています。相当古くから,道のりではなく方角(緯度経度)を使って位置を知る ナビゲーションシステム(山当てという)が,古代の科学の粋であったというのが,私の大学時代の 恩師, 野上道男先生の説で,今年は中止になってしまった京都祇園祭の山車(だし)の先頭の山鉾は 測量道具を象徴しているというのですが,本当でしょうか。
→太陽系の天体の実サイズ模型を作るという動画
最後の方で,ホントの丸い地球を実際に見た人はアポロ宇宙船で月まで行った二十数人の限られた 人々でしかなく,その人たちの感動を(英語ですが)知ってほしいと思いました。 ここまで読んでくれてありがとうございます。
設問の答え→ 400m,日吉キャンパスの下のトンネルのイメージです。